0 概念速记

1. 二元运算：处处定义，函数，封闭
2. 半群：满足结合律，有二元运算
3. 同构：函数，双射，像的积是积的像
4. 同态：处处定义，像的积是积的像
5. 等价：自反，对称，传递
6. 同余关系：等价，$a\ R\ a^\prime \land b\ R\ b^\prime \rightarrow (a\ast b)\ R\ (a^\prime\ast b^\prime)$
7. 群：是半群，满足结合律，存在单位元，存在逆元
8. 子群：存在单位元，封闭，存在逆元

   1 二元运算

$\mathbf{A}$ 上的二元运算是一个处处定义的函数 $f: \mathbf{A} \times \mathbf{A} \rightarrow \mathbf{A}$.

1. $f$ 对于每一个 $(a, b) \in \mathbf{A} \times \mathbf{A}$ 都有定义.
2. 因为 $f$ 是一个函数，所以 $f$ 对于一个 $(a, b) \in \mathbf{A} \times \mathbf{A}$ 只对应 $A$ 中的唯一元素.
3. 封闭：集合中的元素运算后的结果仍然是集合中的元素.

1.1 例子

1. $\mathbb{Z}$ 上的加法运算是一个二元运算.
2. $\mathbb{R}$ 上的除法运算不是一个二元运算，例如 $3\ast 0$ 没有定义，因为 $0$ 不能作除数.
3. $\mathbb{Z}^+$ 上的减法不是二元运算，因为 $2\ast 5 \notin A$.
4. $\mathbb{Z}$ 上的，定义 $a\ast b$ 是比 $a$ 和 $b$ 都小的数，不是二元运算，因为不能唯一对应 $A$ 中的一个元素.

1.2 二元运算的概念

本节中 $a, b, c \in A$, $\ast : A \times A \rightarrow A$.

1.2.1 可交换的(Commutative)

如果一个二元运算是可交换的，则 $a\ast b=b\ast a$ .

当一个二元运算是可交换的当且仅当这个二元运算对应的表关于主对角线对称.

1.2.2 可结合的(Associative)

如果一个二元运算是可结合的，则 $a\ast (b\ast c)=(a\ast b)\ast c$ .

1.2.3 幂等的(Idempotent)

如果一个二元运算是幂等的，则 $a\ast a=a$ .

1.2.4 分配律(Distributive)

如果两个二元运算满足分配率，则 $x\ast(y+z)=(x\ast y)+(x\ast z)$ ，$\ast$ 和 $+$ 是两个不同的二元运算.

1.2.5 德摩根律(De Morgan’s laws)

如果两个二元运算和一个一元运算满足德摩根律

$(x+y)^\ast=x^\ast-y^\ast$ 且 $(x - y)^\ast = x^\ast + y^\ast$

$+,-$是两个不同的二元运算，$\ast $ 是一个一元运算.

2 半群(semigroup)

半群是一个定义了一个可结合的二元运算的非空集合.

半群 $(A, \ast )$ 是由集合 $A$ 和二元运算 $\ast $ 生成的自由半群.

Note: 数域和减法运算不是半群，因为减法运算不是可结合运算。

2.1 单位元(Identity)

若 $x\ast e=e\ast x=x$，则 $e$ 为单位元.

2.1.1 定理

如果 $e$ 是单位元，则 $e$ 是独一无二的.

2.2 逆元(Inverse)

如果 $e$ 是二元运算 $\ast$ 的单位元，并且 $x\ast y=\ast \ast x=e$，则称 $y$ 是 $x$ 的 $\ast $ 逆元，记为 $x^{-1}=y$.

2.3 子半群(subsemigroup)

$(S, \ast )$ 是一个半群，$T$ 是 $S$ 的子集.

如果 $T$ 在运算 $\ast$ 下封闭，则 $(T,\ast )$ 为 $(S, \ast )$ 的子半群.

2.4 独异点、含幺半群(Monoid)

含单位元的半群.

2.5 子独异点(submonoid)

令 $(S, \ast )$ 是一个独异点(或称幺半群)，且 $T$ 是 $S$ 的子集.

如果 $T$ 在运算 $\ast$ 下封闭，并且 $e \in T$，则 $(T, \ast)$ 是 $(S,\ast)$ 的子独异点.

2.6 幂

$(S, \ast )$ 是一个半群，$a \in S$ 且 $n \in \mathbf{Z}$.

$a^0=e, a^1=a, a^n=a^{n-1} \ast a (n \ge 2)$

$a^m \ast a^n = a^{m+n}$

2.7 同构映射(Isomorphism)

令 $(S, \ast), (T, \ast^\prime)$ 是两个半群.

如果函数 $f: S \rightarrow T$ 是 $S$ 到 $T$ 的一一对应的函数并且 $\forall a \in S, b \in S, f(a\ast b)=f(a) \ast^\prime f(b)$，则 $f$ 称为 $(S, \ast )$ 到 $(T, \ast^\prime)$ 的同构映射.

此时 $f^{-1}$也是一个同构映射.

2.7.1 群同构(Isomorphic semigroups)

如果 $f$ 是 $(S, \ast)$ 到 $(T, \ast^\prime)$ 到同构映射，则 $(S, \ast)$ 和 $(T, \ast^\prime)$ 是同构的，记为 $S \cong T$.

2.7.1.1 证明半群同构的方法

STEP 1

定义一个函数 $f: S \rightarrow T, \text{Dom}(f) = S$.

SETP 2

证明 $f$ 是单射且满射的，即证明 $f$ 是双射的.

单射：$\forall t \in T$， 只有一个 $s \in S$ 满足 $f(s) = t$. 证明单射：令 $f(s_1)=f(s_1)$，去证明 $s_1=s_2$ 满射： $\forall t \in T,\exists s \in S, f(s) = t$. 证明满射：任取 $t \in T$，证明存在 $s \in S$，使得 $f(s)=t$

STEP 3

证明 $f(a\ast b)=f(a)\ast^\prime f(b)$.

2.7.2 定理一

如果 $(S, \ast )$ 和 $(T, \ast^\prime)$ 是分别有单位元 $e$ 和 $e’$ 的独异点，并且 $f:S \rightarrow T$ 是同构映射，则 $f(e)=e’$.

Note: 如果 $(S, \ast )$ 和 $(T, \ast^\prime)$ 其中有且仅有一个半群有单位元，那么它们不同构.

2.8 同态映射(Homomorphism)

令 $(S, \ast), (T, \ast^\prime)$ 是两个半群.

如果函数 $f: S \rightarrow T$ 是处处定义的且 $\forall a \in S, b \in S, f(a\ast b)=f(a) \ast^\prime f(b)$，则 $f$ 称为 $(S, \ast )$ 到 $(T, \ast^\prime)$ 的同态映射.

如果 $f$ 还是满射的，则 $T$ 是 $S$ 的同态像(homomorphic image).

同构和同态的差异是：同构必须是单射和满射，两者都需要 “积的像是像的积”。

2.8.1 定理一

如果 $(S, \ast)$ 和 $(T, \ast^\prime)$ 是分别有单位元 $e$ 和 $e’$ 的独异点，并且 $f:S \rightarrow T$ 是满射的同态映射，则 $f(e)=e’$.

2.8.2 定理二

如果 $f$ 是 $(S, \ast)$ 和 $(T, \ast^\prime)$ 的同态关系，并且$S’$ 是 $(S, \ast)$ 的子半群，则 $f$ 下$S’$ 的像 $f(S’)={t \in T\vert t = f(s) \text{ for some } s \in S’}$ 是 $(T, \ast^\prime)$ 的子半群.

2.8.3 定理三

如果 $f$ 是可交换的半群 $(S, \ast)$ 和 $(T, \ast^\prime)$ 的同态关系且是满射，那么 $(T, \ast^\prime)$ 也是可交换的.

2.9 乘积半群(Products of Semigroups)

如果 $(S, \ast)$ 和 $(T, \ast)$ 是半群，则 $(S \times T, \ast^\prime)$ 是半群，$\ast^\prime$ 定义如下：$(s_1, t_1)\ast^\prime(s_2, t_2)=(s_1*s_2, t_1\ast^\prime t_2)$.

如果 $S$ 和 $T$ 是特异点，则 $S \times T$ 也是有单位元 $(e_S, e_T)$ 的特异点.

2.10 同余关系(Congruence relation)

如果 $R$ 是半群 $(S, \ast)$ 上的等价关系，且 $a\ R\ a’ \land b\ R\ b’ \rightarrow (a\ast b)\ R\ (a^\prime\ast b^\prime)$，则 $R$ 是同余关系.

等价关系：具有自反性，对称性，传递性的关系.

等价关系 $R$ 在半群 $(S, \ast )$ 上形成等价类.

$[a]=R(a)$ 是包含 $a$ 的等价类.

$S/R$ 是包含所有等价类的集合.

例如，考虑半群 $(\mathbb{Z},+)$ 和 $\mathbb{Z}$ 上的等价关系 $R$ ，$a\ R\ b$ 当且仅当 $a \equiv b(\mod 2)$.

则 $[0]={0, 2, 4, 8, \cdots}$, $[1]={1, 3, 5, 7, \cdots}$，$\mathbb{Z}/R={[0], [1]}$.

2.10.1 定理一

令 $R$ 是半群 $(S, \ast )$ 上的同余关系，定义关系 $\circledast: S/R \times S/R \rightarrow S/R$， $\circledast([a], [b])=[a]\circledast[b]=[a \ast b]$

则 $(S/R, \circledast)$ 是一个半群，$S/R$ 称为商半群或者因子半群.

推论: 如果 $S$ 是一个特异点，则 $S/R$ 是有单位元 $[e]$ 的特异点.

2.10.2 定理二

$R$ 是半群 $(S, \ast )$ 上的同余关系，$(S/R, \circledast)$ 是对应的商半群，则函数 $f_R: S \rightarrow S/R, f_R(a) = [a]$ 是一个同态关系，且是满射，称为自然同态.

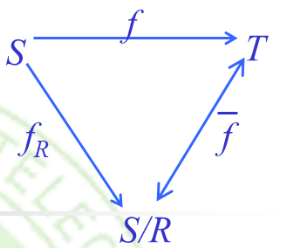
2.11 同态基本定理(FHT)

(Fundamental Homomorphism Theorem, FHT)

令 $f: S \rightarrow T$ 半群 $(S, \ast )$ 到 半群 $(T, \ast^\prime)$ 的同态关系，$R$ 是一个 $S$ 上的关系，定义：$a, b \in \mathbf{S}, a\ R\ b \text{ iff } f(a) = f(b)$.

则 $R$ 是一个同余关系，并且 $(T, \ast^\prime)$ 和商群 $(S/R,\circledast)$ 是同构的，同构函数 $\overline{f}([a])=f(a)$ .

3 群(groups)

群是一个定义了二元运算的集合.

该二元运算满足：

$\forall a,b,c \in G$

1. 满足结合率：$(a\ast b)\ast c = a\ast (b\ast c)$
2. 存在单位元：存在独一无二的元素 $e \in G$ 使得 $\forall a \in G, a\ast e=e\ast a=a$
3. 存在逆元：$\forall a \in G,\exists a^{-1} \in G, a\ast a^{-1}=a^{-1}\ast a=e$

3.1 阿贝尔群

如果 $ab=ba$，则群 $G$ 称为阿贝尔群(Abelian).

3.2 定理一

每个元素只有一个逆元.

3.3 定理二

$ab=ac \rightarrow b=c$ (左消去律) $ba=ca \rightarrow b=c$ (右消去律)

3.4 定理三

$(a^{-1})^{-1}=1$

$(ab)^{-1}=b^{-1}a^{-1}$

3.5 定理四

$ax=b$ 有唯一解

$ya=b$ 有唯一解

3.6 有限群

如果群 $G$ 中的元素有限，则 $G$ 为有限群，$G$ 的阶 $\vert G\vert $ 为 $G$ 的元素数量.

3.7 子群(subgroups)

令 $H$ 为 $G$ 的子集，并且

1. $G$ 的单位元 $e \in H$
2. 如果 $a, b \in H, ab \in H$
3. 如果 $a \in H, a^{-1} \in H$

则 $H$ 称为 $G$ 的子群.

3.7.1 平凡子群(trivial subgroups)

$G$ 和 $H={e}$ 为 $G$ 的平凡子群.

3.7.2 定理一

令 $(G, \ast )$ 和 $(G’, \ast^\prime)$ 是两个群，并且 $f: G \rightarrow G’$ 是同态关系.

则：

1. $e$ 是 $G$ 的单位元，$e’$ 是 $G’$ 的单位元，则 $f(e)=e’$.
2. 如果 $a \in G$, $f(a^{-1})=f^{-1}(a)$.
3. 如果 $H$ 是 $G$ 的子群，则 $f(H)={f(h)\vert h\in H}$ 是 $G’$ 的子群.

3.8 乘积群和商群

如果 $G_1$ 和 $G_2$ 是群，则 $G=G_1 \times G_2$ 也是群，定义在 $G$ 上的二元运算 $\ast$ 定义为：$(a_1,b_1)\ast (a_2,b_2)=(a_1a_2,b_1b_2)$.

例子：$G_1, G_2=\mathbb{Z}_2={[0],[1]}$，$G=G_1 \times G_2={(\overline{0}, \overline{0}), (\overline{1}, \overline{0}), (\overline{0}, \overline{1}), (\overline{1}, \overline{1})}$

Note:

\[\mathbb{Z}_m \times \mathbb{Z}_n \cong \mathbb{Z}_{mn} \text{ iff } \gcd(m, n)=1\]

3.8.1 定理一

$R$ 是群 $(G, \ast )$ 的同余关系，则半群 $(G/R, \circledast)$ 是群， 二元运算 $\circledast$ 的定义如下：$[a] \circledast [b] = [a\ast b]$

$G/N$: $G$ 在 $N$ 上的商群或因子群，在直觉上是把正规子群 $N$ “萎缩”为单位元的群。商群写为 $G/N$ 并念作 $G \mod N$.

3.8.2 推论一

如果$R$ 是群 $(G, \ast )$ 的同余关系，则函数 $f_R: G \rightarrow G/R, f_R(a)=[a]$ 是群同态关系.

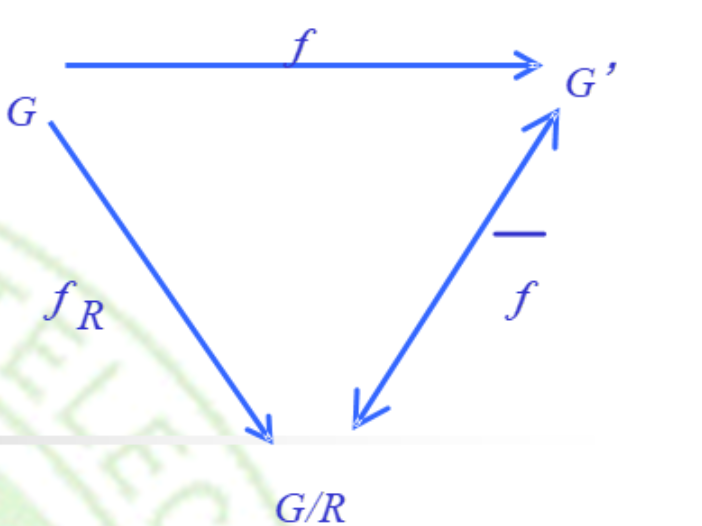
3.8.3 推论二

如果 $f:G \rightarrow G’$ 是群 $(G, \ast )$ 到群 $(G’, \ast^\prime)$ 的同态关系，并且 $R$ 是 $G$ 上的关系，$\forall a, b \in G, a\ R\ b \text{ iff } f(a) = f(b)$.

则：

1. $R$ 是同余关系.
2. 函数 $\overline{f}: G/R \rightarrow G’, \overline{f}([a])=f(a)$ 是群 $(G/R, \circledast)$ 到群 $(G’, \ast^\prime )$ 上同态关系.

3.8.4 正规子群

令 $H$ 为群 $G$ 的子群

3.8.4.1 左陪集

$\forall a \in G, aH = {ah\vert h \in H}$ 是 $H$ 在 $G$ 中由 $a$ 定义的左陪集.

左陪集本质上也是一种等价关系：

令 $b=ah \in aH$，则 $a^{-1}b = h \in H$, 所以 $a\ R\ b$ 当且仅当 $a^{-1}b \in H$，代表元为 $a$.

故左陪集也是 $G$ 的一个划分，$\forall a, b \in G$, $aH$ 和 $bH$ 要么相同(说明 $a\ R\ b$)，要么$aH \cap bH = \emptyset$.

其中，$H$ 自己也是一个左陪集（划分），当 $a=e$, $eH={eh\vert h\in H}=H$.

还要注意的是，$H$ 是所有左右陪集中的唯一的子群.

3.8.4.2 右陪集

$\forall a \in G, Ha={ha\vert h \in H}$ 是 $H$ 在 $G$ 中由 $a$ 定义的右陪集.

右陪集的相关结论和左陪集类似，并且左陪集和右陪集的个数相等.

3.8.4.3 正规子群

若 $\forall a\in G, aH=Ha$, 则 $H$ 为 $G$ 的正规子群.

Note: 如果 $Ha=aH$，不代表 $\forall h \in H, a \in G, ha=ah$

3.8.4.3.1 定理一

若 $R$ 是 $G$ 上的同余关系，$H=[e]$

则 $\forall a\in G, [a]=aH=Ha$，则 $H$ 是正规子群.

3.8.4.3.2 定理二

令 $N$ 是 $G$ 的子群，$R$ 是 $G$ 上的关系，且 $a\ R\ b \text{ iff } a^{-1}b \in N$.

则：

1. $R$ 是 $G$ 上的同余关系
2. $N$ 是等价类 $[e]$

   3.8.4.3.3 定理三

如果 $G$ 是一个阿贝尔群，则 $G$ 的每个子群都是一个正规子群.

3.8.4.3.4 推论一

$f$ 是群 $(G, \ast )$ 到群 $(G’, \ast^\prime )$ 的同态关系，则 $ker(f)={a \in G\vert F(a)=e}$.

$ker(f)$ 是 $G$ 的正规子群并且 $G/ker(f)$ 和 $G’$ 同构.

3.9 一些特殊的群

1. 置换群：
   • 置换群是所有置换构成的群，置换是将一集合元素重新排列的一种映射.在置换群中，群的操作是置换的组合.
   • 对称群 $S_n$ 实际上就是一个置换群的例子，它包含了所有可能的 $n$ 元素置换.其包含了 n 个元素的所有可能排列（置换）.每一个排列都可以看作是一种操作，把一组元素重新排列成另一种顺序.例如，对于三个元素的集合 ${1, 2, 3}$，其对称群 **$S_n$ 包含了所有可能的排列，总共有 $3! = 6$ 种排列.对称群 $S_n$ 有 $n!$ 个元素（因为一个 $n$ 元素集合有 $n!$ 种排列方式）.
2. 循环群：
   • 循环群是由单个元素生成的群，这意味着群内的所有元素都可以通过这个生成元反复进行群操作（比如加法或乘法）得到.
   • 循环群可以是无限的，如整数在加法下构成的群(通常记作 $Z$)，也可以是有限的，如 $Z_n$.$Z_n$ 是由 $n$ 个元素组成的循环群，可以看作是模 $n$ 加法下的整数集合.群中的每个元素可以表示为 ${0, 1, 2, …, n-1}$，群的操作是模 $n$ 的加法.例如，$Z_4$ 中的元素是 ${0, 1, 2, 3}$，而群操作是模 4 加法：$1 + 3 = 0$（因为 $4 \equiv 0 (\mod 4)$）.
   • 一个群是循环的，当且仅当它存在一个元素 $a$，使得群中的每一个元素都可以写成 $a$ 的某个整数次幂.