气体温标
定体气体温标
\[T_V(p)=273.16\lim_{p_0 \to p} \dfrac p{p_0}\]定压气体温标
\[T_p(V)=273.16\lim_{p_0\to0} \dfrac V{V_0}\]理想气体状态方程
\[\begin{gather} pV=vRT \\ pV=\dfrac{N}{N_A}RT \\ p=\dfrac NV\dfrac{R}{N_A}T=nk_BT \end{gather}\]其中 $n$ 是数量密度,即单位体积内有多少个粒子。
理想气体压强和温度的初级微观理论
分子运动论看压强
\[p=\dfrac 1 3 nm\overline{v^2}=\dfrac 2 3 n \overline{\varepsilon_k}\]\(\overline{\varepsilon_k}:\text{分子平均平动动能}\)
温度的微观解释
\[\left. \begin{aligned} p=\dfrac 2 3 n \overline{\varepsilon_k} \\ p=nk_BT \end{aligned} \right\} \Rightarrow \overline{\varepsilon_k}=\dfrac 32k_BT\]麦克斯韦速度分布律
\[\begin{gather} B=\dfrac{m}{2k_BT} \\ C=\left(\dfrac m{2\pi k_BT}\right)^{\frac32} \\ \overline{\varepsilon_k}=\dfrac 3 2k_BT=2\pi mC\dfrac38\sqrt{\dfrac{\pi}{B^5}}\\ \text{速度分布:}f_M(\mathbf{v})=Ce^{-Bv^2} \\ \text{速率分布:}M(v)=4\pi v^2f_M(\mathbf{v}) \end{gather}\]其中 $m$ 是分子的质量。
注意 $F_M(v)$ 仍然是密度函数而不是分布函数。
对于速度分量分布,
\[f_M(\mathbf{v}_i)=\sqrt{\dfrac m{2\pi k_BT}}e^{-\frac{mv_i^2}{2k_BT}}\]其中 $v_i \in {v_x, v_y, v_z}$.
几种统计特征速率
- 最概然速率:$v_p=\sqrt{\dfrac{2RT}{\mu}}=1.41\sqrt{\dfrac{RT}{\mu}}$,$\mu$ 为摩尔质量。
- 平均速率:$\overline{v}=\sqrt{\dfrac{8RT}{\pi\mu}}=1.6\sqrt{\dfrac{RT}{\mu}}$
- 方均根速率:$\sqrt{v^2}=\sqrt{\dfrac{3RT}{\mu}}=1.73\sqrt{\dfrac{RT}{\mu}}$
分子在重力场中密度随高度的等温分布
\[\begin{gather} n(z)=n(0)e^{-\frac{mgz}{k_BT}} \\ p(z)=p(0)e^{-\frac{mgz}{k_BT}} \end{gather}\]推广到任意势能分布:
\[n_B(\mathbf{r})=n_0e^{-\frac{U(\mathbf{r})}{k_BT}}\]故
\[f_{MB}(\mathbf r, \mathbf{v})=n_B(\mathbf{r})f_M(\mathbf{v})=n_0Ce^{-\frac{\varepsilon_k+\varepsilon_p}{k_BT}}\]能量均分定理和热容量
能量按自由度均分定理
\[\overline{v_x^2}=\overline{v_y^2}=\overline{v_z^2}\] \[\overline{\varepsilon}=\dfrac 1 2m\overline{v^2}=\dfrac 3 2 k_BT\] \[\dfrac 1 2m\overline{v_x^2}=\dfrac 1 2m\overline{v_y^2}=\dfrac 1 2m\overline{v_z^2}=\dfrac 12k_BT\]内能
\[U^{mol}=N_A\overline{\varepsilon}=\dfrac 1 2(t+r+2s)N_Ak_BT=\dfrac 1 2 (t+r+2s)RT\]理想气体的定体摩尔热容量和定体比热容
定体摩尔热容量:一摩尔理想气体的定体热容量
\[C_V^{\text{mol}}=\dfrac 1 2(t+r+2s)R\]定体比热容:单位质量的理想气体的比热容
\[c_V=\dfrac 1 \mu C_V^{\text{mol}}\]| 各种气体 | 定体摩尔热容量 |
|---|---|
| 单原子分子理想气体 | $C_V^{\text{mol}}=\dfrac 3 2R$ |
| 刚性双原子分子理想气体 | $C_V^{\text{mol}}=\dfrac 5 2R$ |
| 非刚性双原子分子理想气体 | $C_V^{\text{mol}}=\dfrac 7 2R$ |
| 刚性多原子分子理想气体 | $C_V^{\text{mol}}=3R$ |
热力学第一定律
\[\Delta U=W+Q\]$W$ 为正是外界对系统做功,$Q$ 为正是系统吸热
等体过程
功:
\[W=-\int pdV=0\]吸热:
\[Q=vC_V^{mol}\Delta T\]内能:
\[\Delta U=Q\]等压过程
功:
\[W=-p(V_2-V_1)=-vR(T_2-T1)\]吸热:
\[Q=vC_{p}^{mol}(T_2-T_1)\]内能:
\[\Delta U=vC_V^{mol}(T_2-T_1)=Q+W=vC_{p}^{mol}(T_2-T_1)-vR(T_2-T1)\] \[C_p^{mol}=C_V^{mol}+R\]比热容比:
\(\gamma=\dfrac{C_p^{mol}}{C_V^{mol}}=\dfrac{2+t+r+2s}{t+r+2s}\)
等温过程
功:
\[W=-vRT\ln\dfrac{V_2}{V_1}\]内能:
\[\Delta U=0\]$U^{mol}=\dfrac 1 2 (t+r+2s)RT$ 温度不变,内能不变。
吸热:
\[Q=-W\]绝热过程
过程方程:
\[\begin{gather} pV^{\gamma}=C_1 \\ TV^{\gamma-1}=C_2 \\ \dfrac{p^{\gamma-1}}{T^\gamma}=C_3 \end{gather}\]外界做功:
\[W=\dfrac{(p_2V_2-p_1V_1)}{\gamma-1}\]内能增加:
\[\Delta U=W=\dfrac{p_2V_2-p_1V_1}{\gamma-1}\]多方过程
过程方程:$pV^n=C$
外界做功:$W=\dfrac{(p_2V_2-p_1V_1)}{n-1}$
吸热:$Q=vC_n^{mol}(T_2-T_1)$
内能增加:$\Delta U=vC_V^{mol}(T_2-T_1)$
\[C_n^{mol}=\dfrac{n-\gamma}{n-1}C_V^{mol}\]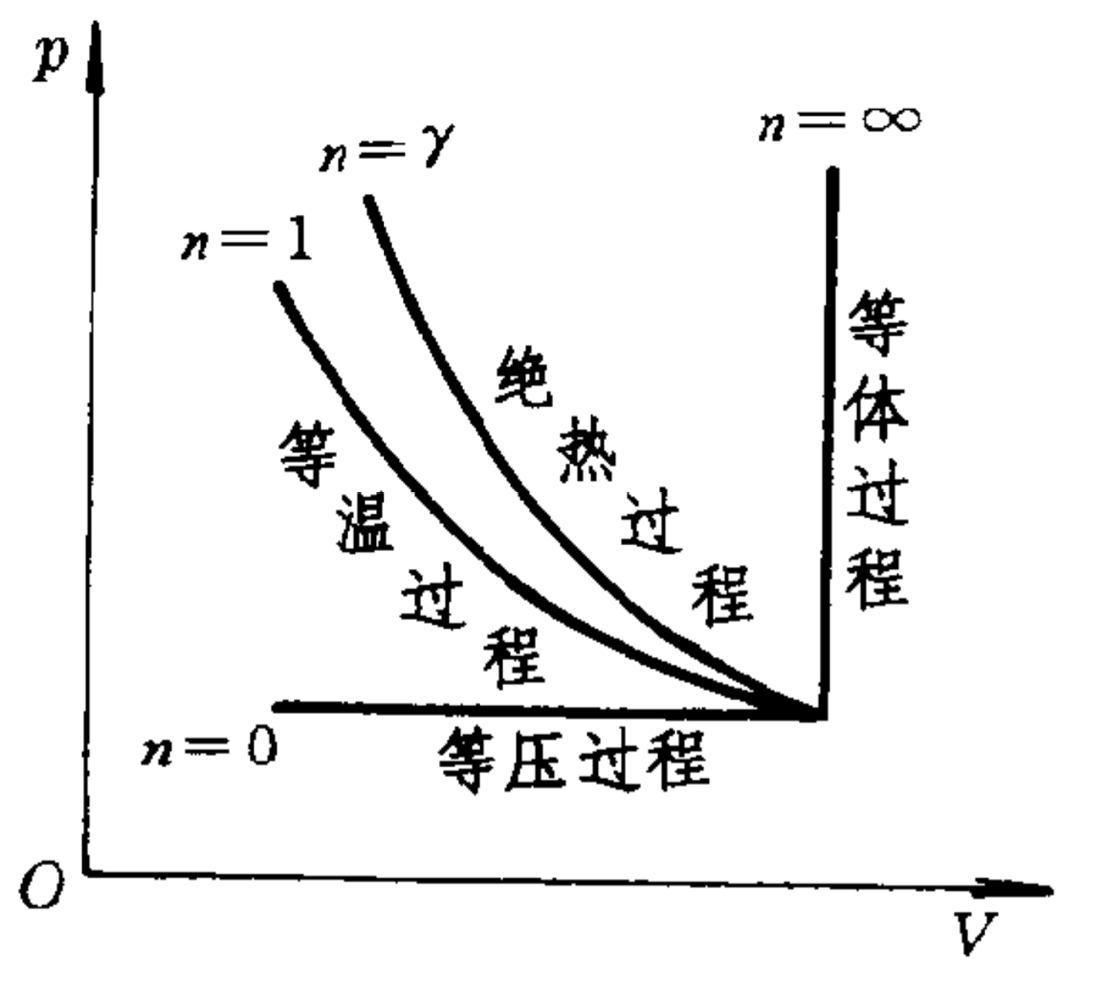
循环过程与卡诺循环
循环
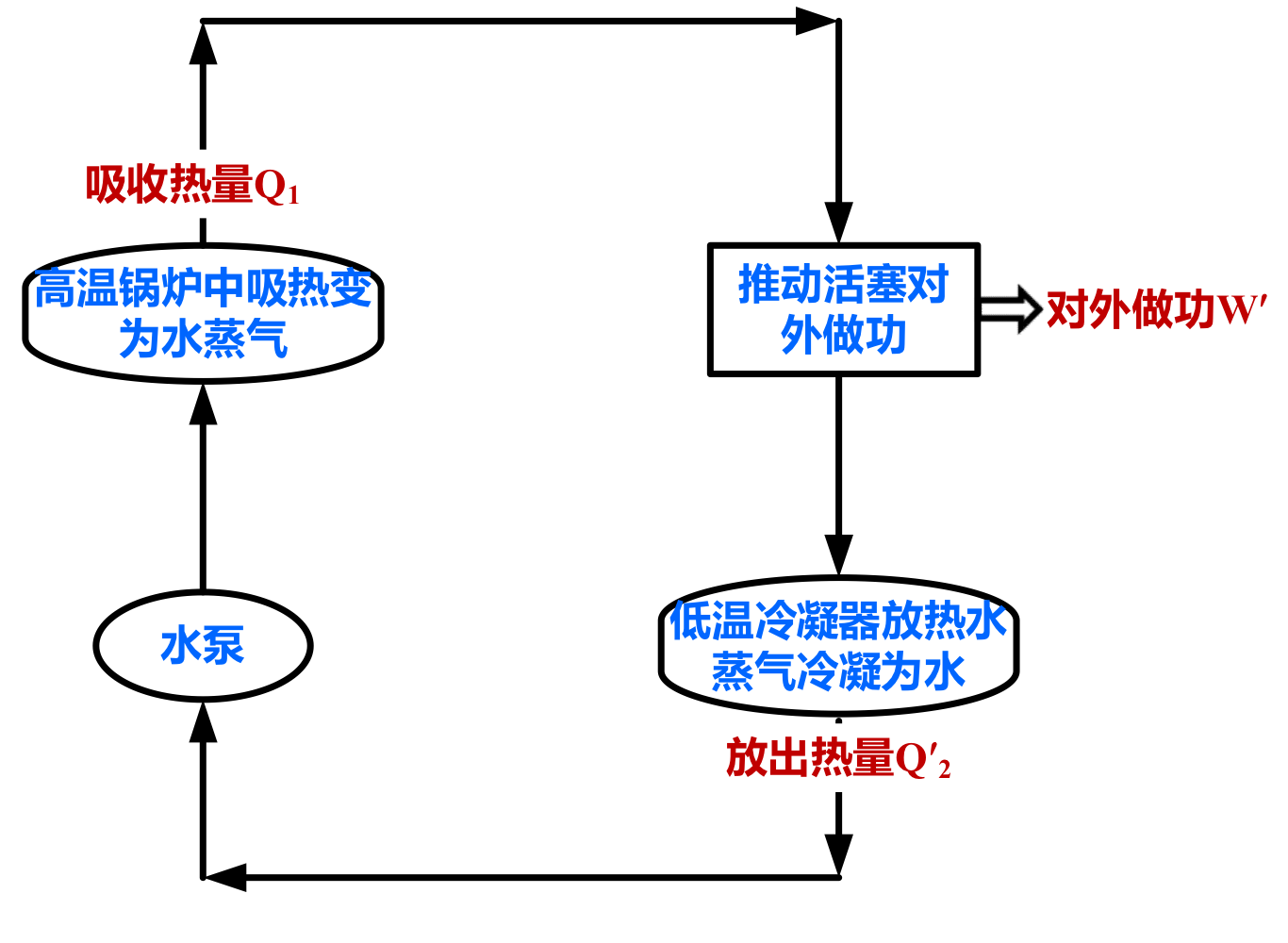
正循环
热机效率:尽可能吸收更少的热量 $Q_1$,获得更大的对外功 $W’$ 的输出。
\[\eta=\dfrac{W'}{Q_1}=\dfrac{Q_1-Q_2^\prime}{Q_1}=1-\dfrac{Q_2^\prime}{Q_1}\]逆循环
制冷效率:尽可能借助更少的外界功 $W$,获得更多的低温热源的吸热 $Q_2$。
\[\varepsilon=\dfrac{Q_2}W=\dfrac{Q_2}{Q_1^\prime-Q_2}\]