光学

1 光学导言

1.1 惠更斯原理

入射角等于反射角 $i=i’$

入射角和折射角：$i\sin i=r \sin r$

$v=\dfrac c n$

1.2 光波的描述

光强和电矢量振幅的二次方成正比：$I=\dfrac n {2c\mu_0}E_0^2 \propto nE_0^2$

在比较两种介质的光强的时候，注意：$I=nE_0^2$

1.3 简谐波的数学表达式

二维

\[\begin{aligned} U&=A\cos \left[ \omega(t\mp\dfrac x v) + \phi \right]\\ &=A\cos(\omega t\mp kx+\phi) \end{aligned}\]

其中 $k=\dfrac{2\pi}\lambda$ 为波数，$\mp$ 为正时，向 $x$ 轴负方向传播，为负时，向 $x$ 轴正方向传播。

三维

\[\begin{aligned} U=A\cos(\omega t \mp \mathbf{k} \cdot \mathbf{r}) \end{aligned}\]

其中 $\mathbf{k} = \dfrac {2\pi} \lambda \mathbf{n}$，$\mp$ 为正时，向 $\mathbf{n}$ 负方向传播，为负时，向 $\mathbf{n}$ 正方向传播。

$\lambda$ 为空间周期，$\mathbf{k}$ 为空间角频率，$\mathbf{k}=k_x\hat{e}_x+k_y\hat{e}_y+k_z\hat{e}_z$

球面波

\[\begin{aligned} U(r,t)&=A\cos(\omega t\mp kr)\\ &=\dfrac{A_0}{r}\cos(\omega t\mp kr) \end{aligned}\]

负号为发散波，正号为汇聚波，$A$ 是球面波传播到 $r$ 处的振幅，$A_0$ 是离波源单位距离处的振幅。

在 $z$ 轴附近的傍轴近似：

\[U=\dfrac A z\cos\left[\omega t\mp k\left(z+\frac{x^2+y^2}{2z}\right)\right]\]

复数表示

\[\widetilde{U}(P,t)=Ae^{i\phi(P)} \cdot e^{-i\omega t} = \widetilde{U}(P)e^{-i\omega t}\]

平面波的复振幅： $\widetilde{U}(P)=Ae^{i\phi(P)}=Ae^{i\mathbf{k}\cdot\mathbf{r}}$

从原点发散开来的球面波，复振幅为 $\widetilde{U_1}(P)=\dfrac {A_1} r e^{ikr}, r=\sqrt{x^2+y^2+z^2}$.

汇聚到原点的球面波，复振幅为 $\widetilde{U_2}(P)=\dfrac {A_1} r e^{-ikr}, r=\sqrt{x^2+y^2+z^2}$.

2 光在各项同向介质界面上的反射与折射

2.1 一些公式

	$s$ 分量	$p$ 分量
振幅反射率	$r_s=-\dfrac{E^\prime_{1s}}{E_{1s}}=-\dfrac{\sin(i_1-i_2)}{\sin(i_1+i_2)}$	$r_p=\dfrac{E^\prime_{1p}}{E_{1p}}=-\dfrac{\tan(i_1-i_2)}{\sin(i_1+i_2)}$
振幅透射率	$t_s=\dfrac{E_{2s}}{E_{1s}}=\dfrac{2\cos{i_1}\sin{i_2}}{\sin(i_1+i_2)}$	$t_p=\dfrac{E_{2s}}{E_{1s}}=\dfrac{2n_1\cos{i_1}}{n_2\cos{i_1}+n_1\cos{i_2}}$
光强反射率	$R_s=\dfrac{I^\prime_{1s}}{I_{1s}}=\vert r_s\vert^2$	$R_p=\dfrac{I^\prime_{1p}}{I_{1p}}=\vert r_p\vert^2$
光强透射率	$T_s=\dfrac{I_{2s}}{I_{1s}}=\dfrac{n_2}{n_1} \vert t_s \vert^2$	$T_p=\dfrac{I_{2p}}{I_{1p}}=\dfrac{n_2}{n_1} \vert t_p \vert^2$
光功率反射率	$\mathscr{R}_s=\dfrac{W^\prime_{1s}}{W_{1s}}=R_s$	$\mathscr{R}_p=\dfrac{W^\prime_{1p}}{W_{1p}}=R_p$
光功率透射率	$\mathscr{T}_s=\dfrac{W_{2s}}{W_{1s}}=\dfrac{\cos{i_2}}{\cos{i_1}}T_s$	$\mathscr{T}_p=\dfrac{W_{2p}}{W_{1p}}=\dfrac{\cos{i_2}}{\cos{i_1}}T_p$

注：

光强$I$的含义是平均能流密度，$I=\dfrac{n}{2c\mu_0}\vert E\vert ^2\propto n\vert E\vert ^2$，因为反射光和入射光在同一个介质中，所以 $R=\dfrac{I^\prime_{1}}{I_{1}}=\vert r\vert ^2$ ，而透射光和入射光在不同介质中，所以 $T=\dfrac{n_2}{n_1}\vert t\vert ^2$ 。
光功率 $W$ 等于光强$I$ 与光通截面 $S$ 的乘积，由反射定律和折射定律可知，反射光束与入射光束的横截面相等，而折射光束与入射光束的截面之比为 $\dfrac{\cos{i_2}}{\cos{i_1}}$，因此有 $\mathscr{R}=R,\mathscr{T}=\dfrac{\cos{i_2}}{\cos{i_1}}T$
根据能量守恒，对于 $p, s$ 分量分别有
\[W'_{1p}+W_{2p}=W_{1p}, {W'_{1s}+W_{2s}=W_{1s}}\]
进而得出
\[R_p+\dfrac{\cos{i_2}}{\cos{i_1}}T_p=1, R_s+\dfrac{\cos{i_2}}{\cos{i_1}}T_s=1\] \[|r_p|^2+\dfrac{n_2\cos_{i_2}}{n_1\cos{i_1}}|t_p|^2=1, |r_s|^2+\dfrac{n_2\cos_{i_2}}{n_1\cos{i_1}}|t_s|^2=1\]
对于 $r_s$，外反射有相位突变 $\pi$，内反射无相位突变，$t_s$ 均没有相位突变。$r_p$ 在经过布儒斯特角($\theta_1+\theta_2=\pi$)后有相位突变，透射没有。

2.2 布儒斯特定律

从 $n_1$ 射向 $n_2$，当反射光完全偏振时，入射角称为布儒斯特角，也称为起偏振角

\[\tan{\theta_B}=\dfrac{n_2}{n_1}\]

2 干涉

光程差 $\delta=n \cdot \Delta r = m \lambda (m=0,1,2,\cdots)$ 时相长干涉

$\Delta r=\dfrac{\Delta y \cdot d}{D}$ (几何关系)

故 $\delta = n \cdot \dfrac{\Delta y \cdot d}{D}=m\lambda$ ，$\Delta y= \dfrac{m\lambda D}{n d}$

明条纹位置：

\[\begin{cases}\Delta\varphi =\pm m\pi \\ \delta = \pm m \lambda \\ y = \pm m \dfrac {D\lambda} d \end{cases}\]

暗条纹位置：

\[\begin{cases}\Delta\varphi =\pm (2m-1)\pi \\ \delta = \pm (2m-1) \dfrac \lambda 2 \\ y = \pm (2m-1)\dfrac {D\lambda} {2d} \end{cases}\]

若光源向上偏移对称轴 $x$ ，则条纹整体下移 $\dfrac {Dx} B$

相邻条纹之间的距离 $\dfrac{D\lambda}d$

2.1 等倾干涉

在入射时可能不能认为是垂直入射。

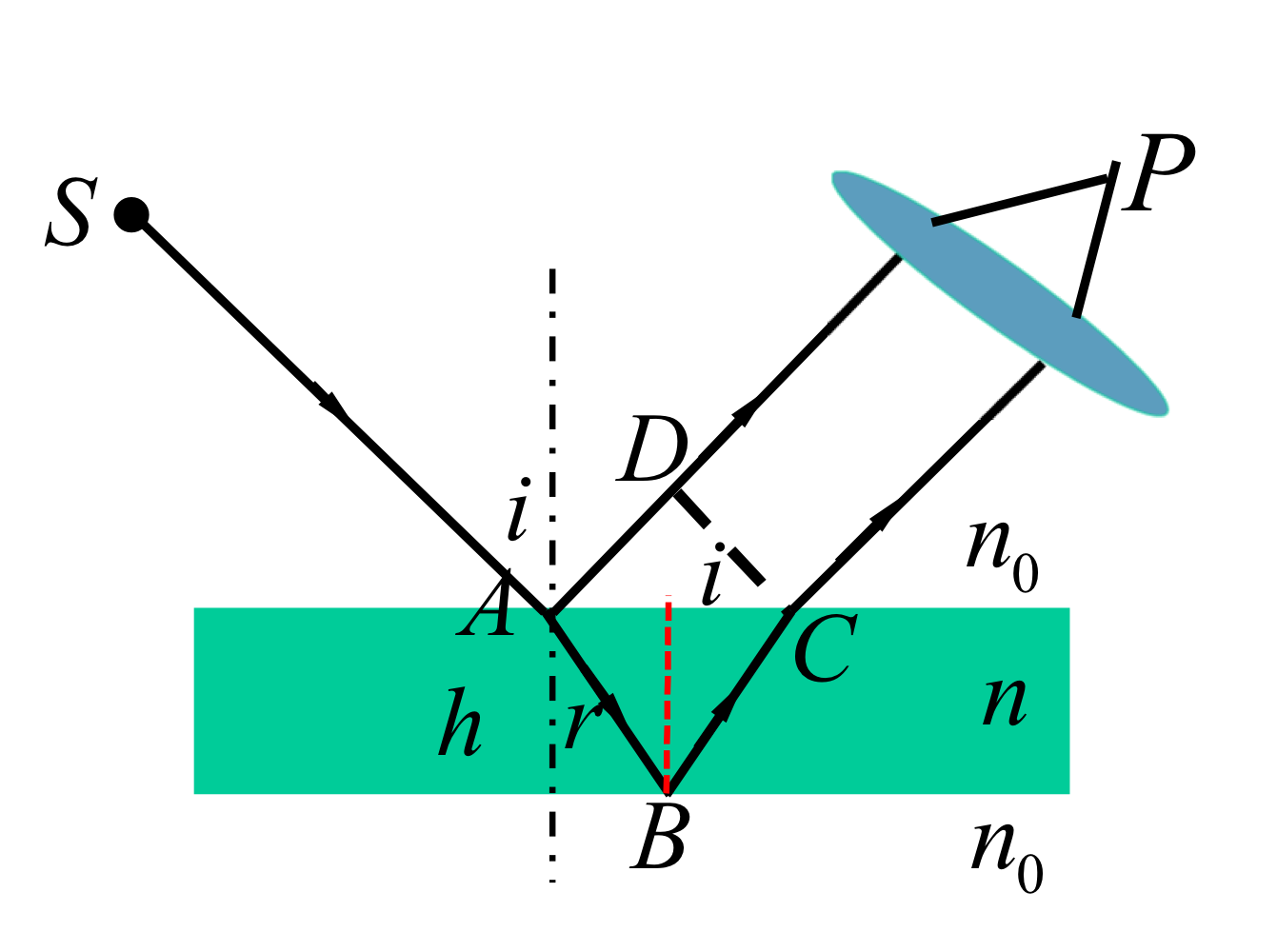要乘 $\cos r$： $\delta=2nh\cos r\pm \dfrac \lambda 2$

等厚干涉的式子相同。

2.2 牛顿环

$r=\sqrt{2Rh}$ （几何关系）

明环：$2nh+\dfrac \lambda 2=m \lambda \rightarrow r_{m\text{明}}=\sqrt{\dfrac {(2m-1)R\lambda} 2}$

暗环：$2nh+\dfrac \lambda 2=(2m+1)\dfrac \lambda 2 \rightarrow r_{m暗}=\sqrt{mR\lambda}$

3 衍射

3.1 夫琅禾费单缝衍射

\[\begin{cases} a\sin \theta=\pm m \lambda &, \text{P 点为暗纹} \\ a\sin \theta=\pm (2m-1) \dfrac \lambda 2&, \text{P 点为明纹} \\ a\sin \theta=0 &, \text{P 点为零级强明纹} \\ \end{cases}\] \[I=I_0(\dfrac {\sin \alpha} \alpha)^2, 2\alpha=\dfrac{2\pi}\lambda a\sin\theta\]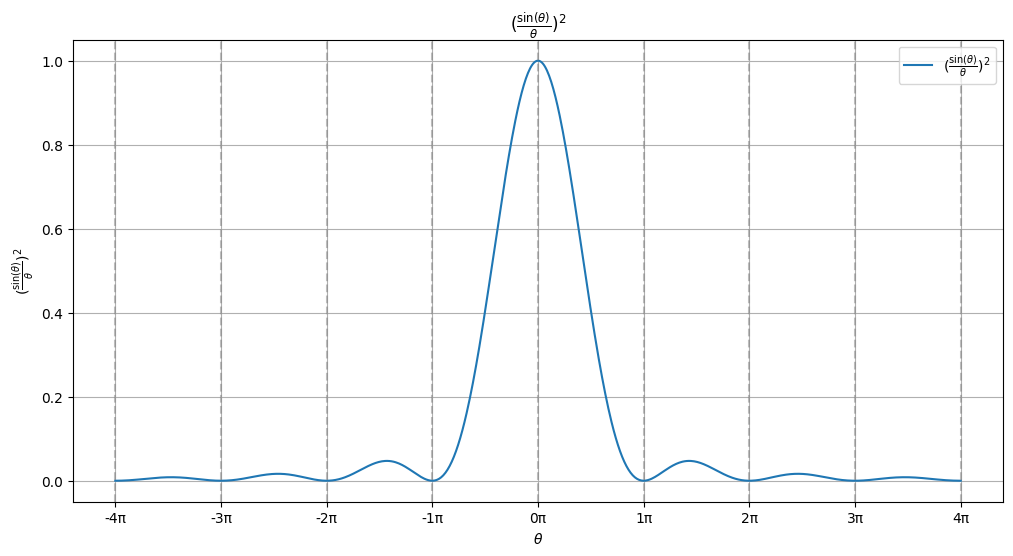

3.2 光栅衍射

光栅方程：$d\sin\theta=\pm m\lambda$

光栅参数：$d$ 为相邻缝之间的距离。

角色散

$d\sin\theta=m\lambda$ 两边做全微分

\[d\cos\theta\mathbf{d}\theta=m\mathbf{d}\lambda\] \[D=\dfrac{\mathbf{d}\theta}{\mathbf{d}\cos{\theta}}=\dfrac{m}{d\cos\theta}\]

为单位波长间隔造成的色散角度。

色分辨本领

相邻两条谱线经过光栅后的主极大可能会十分靠近，判断是否能分辨的是瑞利判据。

\[\Delta\lambda=\dfrac{\lambda}{kN}\]

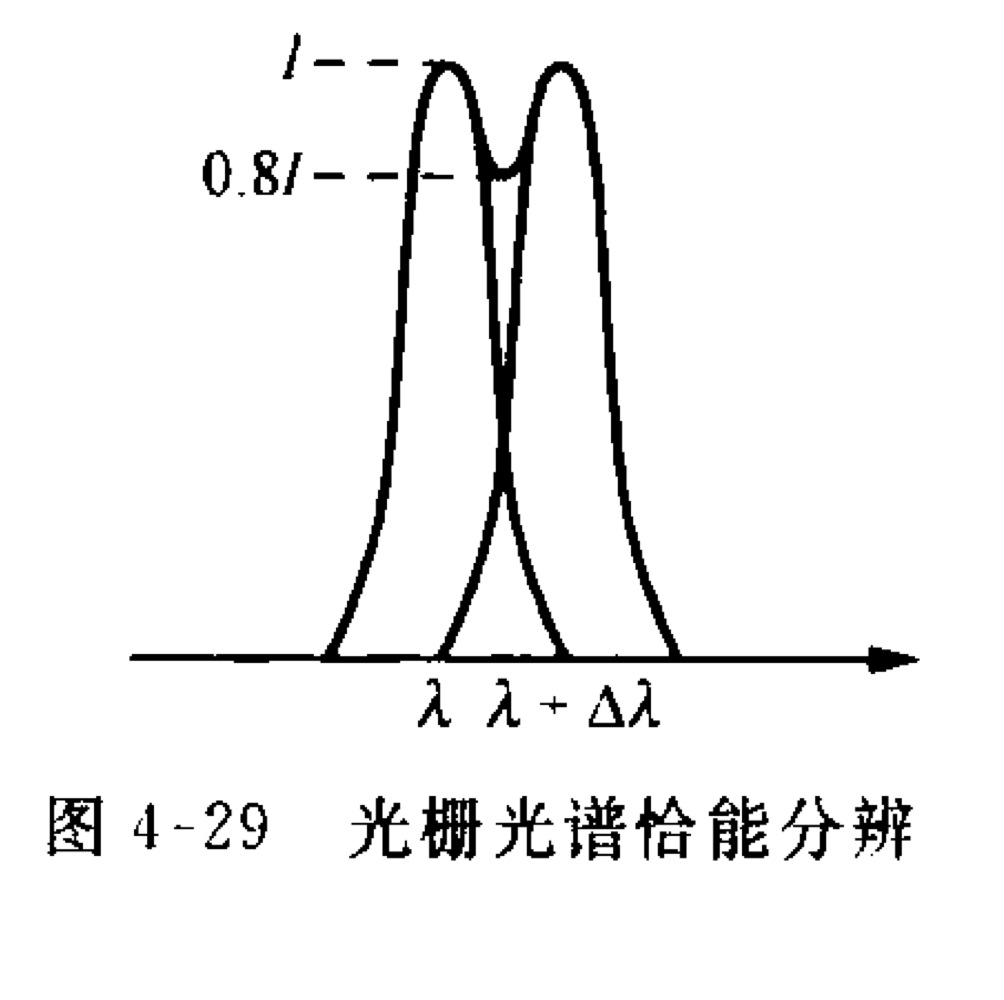
主极大半角宽度

\[\Delta \theta=\dfrac{\lambda}{Nd\cos\theta}\]

波列长度

\[L=\dfrac{\lambda^2}{\Delta \lambda}\]

$\Delta\lambda$ 是波长的变化范围。

4 偏振

方位角：光矢量(E)与入射面的夹角。

当入射光为线偏振光并且方位角是 $\alpha$ 时，反射率 $\mathscr{R}$ 和折射率 $\mathscr{T}$ 满足：

\[\mathscr{R}=\mathscr{R}_p\cos^2\alpha+\mathscr{R}_s\sin^2\alpha\] \[\mathscr{T}=\mathscr{T}_p\cos^2\alpha+\mathscr{T}_s\sin^2\alpha\]

一束光入射偏振片，振动方向和偏振片方向相差 $\theta$：

\[I=I_0\cos^2\theta\]

如果入射光是自然光，则

\[\mathscr{R}=\dfrac 1 2(\mathscr{R}_p+\mathscr{R}_s)\] \[\mathscr{T}=\dfrac 1 2(\mathscr{T}_p+\mathscr{T}_s)\] \[I=\dfrac{I_0}2\]

双折射

一束光进入(特殊)晶体出现两束折射光，一束为寻常(ordinary)光：o光，另一束为非寻常(extraordinary)光：e光。

光轴为晶体中的特殊方向，光沿此方向传播不发生双折射（e光在此方向传播速度和 o 光相同）。

光轴与 o 光组成的平面称为 o 光主平面，o光振动方向垂直 o 光主平面。 o 光在各个方向传播速度相等，为 $\dfrac{c}{n_o}$。

光轴与 e 光组成的平面称为 e 光主平面，e 光振动方向在 e 光主平面内。e 光在光轴方向传播速度为 $\dfrac{c}{n_o}$，在垂直光轴方向传播速度为 $\dfrac{c}{n_e}$。

对于负单轴晶体，$n_o>n_e$，e 光垂直于光轴的方向速度比 o 光快，光轴是慢轴。

对于正单轴晶体，$n_o < n_e$，e 光垂直于光轴的方向速度比 o 光慢，光轴是快轴。

	$s$ 分量	$p$ 分量
振幅反射率	\(r_s=-\dfrac{E^\prime_{1s}}{E_{1s}}=-\dfrac{\sin(i_1-i_2)}{\sin(i_1+i_2)}\)	\(r_p=\dfrac{E^\prime_{1p}}{E_{1p}}=-\dfrac{\tan(i_1-i_2)}{\sin(i_1+i_2)}\)
振幅透射率	\(t_s=\dfrac{E_{2s}}{E_{1s}}=\dfrac{2\cos{i_1}\sin{i_2}}{\sin(i_1+i_2)}\)	\(t_p=\dfrac{E_{2s}}{E_{1s}}=\dfrac{2n_1\cos{i_1}}{n_2\cos{i_1}+n_1\cos{i_2}}\)
光强反射率	\(R_s=\dfrac{I^\prime_{1s}}{I_{1s}}=\vert r_s\vert^2\)	\(R_p=\dfrac{I^\prime_{1p}}{I_{1p}}=\vert r_p\vert^2\)
光强透射率	\(T_s=\dfrac{I_{2s}}{I_{1s}}=\dfrac{n_2}{n_1} \vert t_s \vert^2\)	\(T_p=\dfrac{I_{2p}}{I_{1p}}=\dfrac{n_2}{n_1} \vert t_p \vert^2\)
光功率反射率	\(\mathscr{R}_s=\dfrac{W^\prime_{1s}}{W_{1s}}=R_s\)	\(\mathscr{R}_p=\dfrac{W^\prime_{1p}}{W_{1p}}=R_p\)
光功率透射率	\(\mathscr{T}_s=\dfrac{W_{2s}}{W_{1s}}=\dfrac{\cos{i_2}}{\cos{i_1}}T_s\)	\(\mathscr{T}_p=\dfrac{W_{2p}}{W_{1p}}=\dfrac{\cos{i_2}}{\cos{i_1}}T_p\)