定义
\[\text{令} s=\sigma+j\omega, z=e^{sT}\]\(X(z)=\sum_{n=-\infty}^{\infty} x(n) z^{-n}\)
单边 $z$ 变换
\(X(z)=\sum_{n=0}^{\infty}x(n)z^{-n}\)
收敛域
对于任意给定的序列 $x(n)$,能使
\[X(z)=\sum_{n=-\infty}^{\infty}x(n)z^{-n}\]收敛的所有 $z$ 值之集合为收敛域。
即满足 $\sum_{n=-\infty}^{\infty}\vert x(n) z^{-n} \vert < \infty$ 的区域。
- 收敛域为 $z$ 平面上以原点为中心的圆环
- 收敛域内不包含任何极点(以极点为边界)
- 有限长序列的收敛域为整个 $z$ 平面(可能除去 $z=0$ 和 $\vert z \vert = \infty$)
- 右边序列的收敛域为 $\vert z \vert = R_1$ 的圆外
- 左边序列的收敛域为 $\vert z \vert=R_2$ 的圆内
- 双边序列的收敛域为 $R_1 < \vert z \vert < R_2$ 的圆环
典型信号的 $z$ 变换
1. 单位样值序列
\[\delta(n)=\begin{cases}1, &n=0\\ 0, &n \neq 0 \end{cases}\] \[X(z)=\sum_{n=\infty}^{\infty}\delta(n)z^{-n}=1\]ROC: 整个$z$ 平面。
2. 单位阶跃序列
\[u(n)=\begin{cases}1, &n\ge0\\ 0, &n < 0 \end{cases}\]\(X(z)=\sum_{n=-\infty}^{\infty}x(n)z^{-n}=\dfrac z{z-1}\) ROC: $\vert z\vert > 1$
3. 斜变序列的 $z$ 变换
\[x(n)=nu(n)\] \[X(z)=\sum_{n=0}^{\infty}nz^{-n}=\dfrac z{(z-1)^2}\]ROC: $\vert z\vert > 1$
4. 指数序列
右边序列 $x(n)=a^nu(n)$
\[X(z)=\sum_{n=0}^{\infty}a^nz^{-n}=\dfrac z{z-a}\]ROC: $\vert z\vert >\vert a\vert$
左边序列 $x(n)=-a^nu(-n-1)$
\[X(z)=-\sum_{n=-\infty}^{-1}a^nz^{-n}=\dfrac z{z-a}\]ROC: $\vert z\vert < \vert a\vert$
$z$ 变换的性质
1. 线性性质
若 $\mathscr{Z}[x(n)]=X(z)$, $\mathscr{Z}[y(n)]=Y(z)$
则 $\mathscr{Z}[ax(n)+by(n)]=aX(z)+bY(z)$
ROC: 一般情况下取重叠部分,根据收敛域中不包括任何一个极点判断
2. 位移性质
2.1 双边 $z$ 变换的位移性质
若$\mathscr{Z}[x(n)]=X(z)$,则$\mathscr{Z}[x(n-m)]=z^{-m}X(z)$
$m$ 为整数
收敛域:只会影响 $z=0,z=\infty$ 处
2.2 单边 $z$ 变换的位移性质
若 $x(n)$ 为双边序列,其单边 $z$ 变换为 $\mathscr{Z}[x(n)u(n)]$
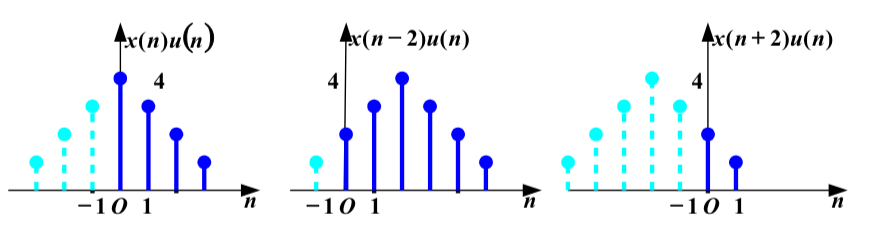
$x(n-m)u(n), x(n+m)u(n)$ 较 $x(n)u(n)$ 的长度有所增减。
a. 右移位性质
若 $\mathscr{Z}[x(n)u(n)]=X(z)$
则
\[\mathscr{Z}[x(n-m)u(n)]=z^{-m}[X(z)+\sum_{k=-m}^{-1}x(k)z^{-k}]\]b. 左移位性质
若 $\mathscr{Z}[x(n)u(n)]=X(z)$
则
\[\mathscr{Z}[x(n+m)u(n)]=z^m[X(z)-\sum_{k=0}^{m-1}x(k)z^{-k}]\]3. 序列线性加权
若 $\mathscr{Z}[x(n)]=X(z)$
则 $nx(n) \leftrightarrow z^{-1} \dfrac{\mathbf{d}X(z)}{\mathbf{d}z^{-1}}$
$n^mx(n) \leftrightarrow [-z\dfrac {\mathbf{d}}{\mathbf{d}z}]^mX(z)$
4. 序列指数加权
若 $\mathscr{Z}[x(n)]=X(z)$
则 $a^nx(n) \leftrightarrow X(\dfrac z a)$
5. 初值定理
若 $x(n)$ 为因果序列。
已知
\[X(z)=\mathscr{Z}[x(n)]=\sum_{n=0}^{\infty}x(n)z^{-n}\]则
\[x(0)=\lim_{z \to \infty}X(z)\]6. 终值定理
若 $x(n)$ 为因果序列,已知
\[X(z)=\mathscr{Z}[x(n)]=\sum_{n=0}^{\infty}x(n)z^{-n}\]则
\[\lim_{n \to \infty}x(n)=\lim_{z \to 1}[(z-1)X(z)]\]终值定理存在的条件:
-
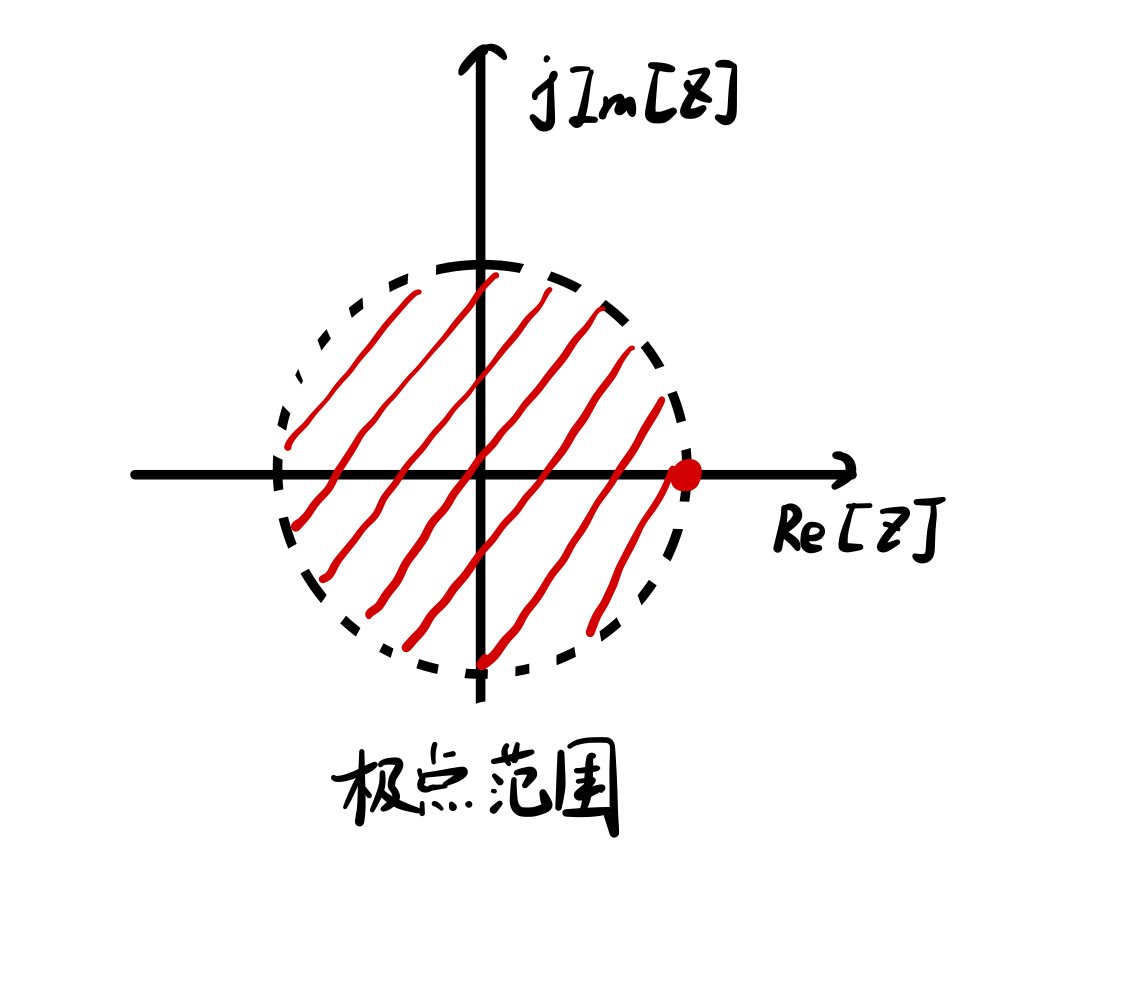
$X(z)$ 的极点位于单位圆内,收敛半径小于1,有终值
\[x(\infty)=\lim_{z \to 1}(z-1)X(z)=0\] -
若极点位于单位圆上,只能位于 $z=1$,并且是一阶极点。
\[x(\infty)=\lim_{z \to 1}(z-1)X(z)\]
7. 时域卷积定理
已知 $X(z)=\mathscr{Z}[x(n)], H(z)=\mathscr{Z}[h(n)]$
则 $\mathscr{Z}[x(n)*h(n)]=X(z)H(z)$
ROC: 一般情况下取重叠部分.
8. $z$ 域卷积定理*
逆 $z$ 变换
只介绍部分分式展开法。
1. 预处理
先把 $X(z)$ 乘 $z^{-1}$
2. 部分分式展开
展开部分分式,使用掩盖法求系数。这一步和拉普拉斯逆变换的部分分式展开法类似。
注意对于高阶极点,需要额外处理。
\[X(z)=\sum_{j=1}^s\dfrac{B_jz}{(z-z_i)^j}\]其中
\[B_j=\dfrac 1{(s-j)!}\left[\dfrac{\mathbf{d}^{s-j}}{\mathbf{d}z^{s-j}}(z-z_i)^s\dfrac{X(z)}z\right]\]例如:
\[\dfrac{X(z)}z=\dfrac 1{z(z-1)^2}=\dfrac{B_1}{z-1}+\dfrac{B_2}{(z-1)^2}+\dfrac{B_3}z\]其中,$B_2, B_3$ 直接利用掩盖法计算。
\[B_1=\dfrac 1{(2-1)!}\left[\dfrac{\mathbf{d}^{2-1}}{\mathbf{d}z^{2-1}}(z-1)^2\dfrac{X(z)}z\right]_{z=1}=-1\]这里和拉普拉斯逆变换的高阶极点处理方式也类似。
3. 查表
查表把展开的部分分式对应到原函数。
$z$ 变换求解差分方程
对方程两边进行单边 $z$ 变换,注意2.2 单边 $z$ 变换的位移性质
\[\mathscr{L}[x(n-m)u(n)]=z^{-m}\left[X(z)+\sum_{k=-m}^{-1}x(k)z^{-k}\right]\]求出 $Y(z)$,再逆变换得 $y(n)$。