拉普拉斯变换的定义

双边拉普拉斯变换

\[F(s)=\mathscr{L}[f(t)]=\int_{-\infty}^{+\infty}f(t)e^{-st}dt\] \[f(t)=\mathscr{L}^{-1}[F(s)]=\dfrac 1{2 \pi j}\int_{\sigma-j\ \infty}^{\sigma+j\ \infty}F(s)e^{st}ds\]

其中 $s=\sigma+j\omega$， 记作 $f(t) \overset{LT}{\leftrightarrow}F(s)$.

单边拉普拉斯变换

\[F(s)=\mathscr{L}[f(t)]=\int_{\color{red}0^-}^{+\infty}f(t)e^{-st}dt\]

推导过程

考虑到

\[\mathscr{F}[f(t)]=\int_{-\infty}^{\infty}f(t)e^{-j\omega t}\mathbf{d}t\]

$f(t)$ 有的时候不满足可积条件，故乘以衰减因子 $e^{-\sigma t}, \sigma \in \mathbb{R}$，当 $\sigma$ 取合适的值时，容易满足可积条件。

\[\mathscr{L}[f(t)]=\mathscr{F}[f(t)\cdot e^{-\sigma t}]=\int_{-\infty}^{+\infty}f(t)e^{-\sigma-j\omega t}dt=F(\sigma+j\omega)=F(s)\]

拉普拉斯变换的收敛域

使 $F(s)$ 存在的 $s$ 的区域称为收敛域，记为 ROC.

1. $f(t)$ 为右边信号，若对 $\sigma > \sigma_1$ 的所有实数满足

   \[\lim_{t \rightarrow \infty} f(t) \cdot e^{-\sigma t}=0\]

   ROC: $Re[s]=\sigma > \sigma_1$

2. $f(t)$ 为右边信号，若对 $\sigma < \sigma_2$ 的所有实数满足

   \[\lim_{t\rightarrow-\infty}f(t) \cdot e^{-\sigma t}=0\]

   ROC: $Re[s]=\sigma < \sigma_2$

3. 双边信号的收敛域为两个收敛域的子集，ROC: $\sigma_1 < \sigma < \sigma_2$.

常用信号的拉普拉斯变换

1. 阶跃函数

\[\mathscr{L}[u(t)]=\dfrac 1 s\]

ROC: $\sigma > 0$

2. 单边指数函数

\[\mathscr{L}[e^{-s_0t}u(t)]=\dfrac 1{s + s_0}\]

$s_0=\alpha+j\omega_0$, ROC: $\sigma > -Re[s]$ 即 $\sigma > -\alpha$.

3. 单位冲激信号

\[\mathscr{L}[\delta(t)]=1\]

ROC: 全 $s$ 域平面收敛.

4. $t^nu(t)$

\[\mathscr{L}[t^nu(t)]=\dfrac{n!}{s^{n+1}}\]

ROC: $\sigma > 0$.

5. 三角函数

\[\mathscr{L}[{\sin(\omega_0t)}]=\dfrac{\omega_0}{s^2+\omega_0^2}\] \[\mathscr{L}[\cos(\omega_0t)]=\dfrac{s}{s^2+\omega_0^2}\]

ROC: $\sigma>0$.

6. 冲击偶信号

\[\mathscr{L}[\delta’(t)]=s\]

典型信号拉氏变换表

拉普拉斯变换的性质

1. 线性性质

若 $\mathscr{L}[f_1(t)]=F_1(s)$, $\mathscr{L}[f_2(t)]=F_2(s)$，则 $\mathscr{L}[K_1f_1(t)+K_2f_2(t)]=K_1F_1(s)+K_2F_2(s)$

收敛域取交集，不包含任何一个极点.

2. 时移性质

若 $\mathscr{L}[f(t)]=F(s)$，则 $\mathscr{L}[f(t-t_0)u(t-t_0)]=F(s)e^{-st_0}$.

$t_0>0$，需要取单边.

3. s 域平移性质

若 $\mathscr{L}[f(t)]=F(s)$, 则 $\mathscr{L}[f(t)e^{-at}]=F(s+a)$.

4. 尺度变换性质

若 $\mathscr{L}[f(t)]=F(s)$, 则 $\mathscr{L}[f(at)]=\dfrac 1 a F(\dfrac s a), (a > 0)$

Note: 时移和尺度变换都有时：$\mathscr{L}[f(at-b)u(at-b)]=\dfrac 1 a F(\dfrac s a)e^{-s \frac b a}$.

5 卷积定理

若 $\mathscr{L}[f_1(t)]=F_1(s)$, $\mathscr{L}[f_2(t)]=F_2(s)$, $f_1(t)$, $f_2(t)$ 为有始信号，则

\[\mathscr{L}[f_1(t) * f_2(t)]=F_1(s)F_2(s)\] \[\mathscr{L}[f_1(t)f_2(t)]=\dfrac 1 {2\pi j}F_1(s)*f_2(s)\]

6. 微分性质

(1) 双边拉普拉斯变换

若 $\mathscr{L}[f(t)]=F(s)$，则 $\mathscr{L}[\dfrac{\mathrm{d}f(t)}{\mathrm{d}t}]=sF(s)$

(2) 单边拉普拉斯变换

若 $\mathscr{L}[f(t)]=F(s)$，则 $\mathscr{L}[\dfrac{\mathrm{d}f(t)}{\mathrm{d}t}]=sF(s)-f(0_-)$

7. 积分性质

(1) 双边拉普拉斯变换

若 $\mathscr{L}[f(t)]=F(s)$，则 $\mathscr{L}[\int_{-\infty}^{t}f(\tau)\mathrm{d}\tau]=\dfrac{F(s)}s$

(2) 单边拉普拉斯变换

若 $\mathscr{L}[f(t)]=F(s)$，则 $\mathscr{L}[\int_{-\infty}^{t}f(\tau)\mathrm{d}\tau]=\dfrac{F(s)}s+\dfrac{f^{(-1)}(0_-)}s$

8. 初值定理

若 $f(t)$ 及 $\dfrac{\mathrm{d}f(t)}{\mathrm{d}t}$ 可以进行拉氏变换，且 $f(t) \leftrightarrow F(s)$，则

\[\lim_{t \rightarrow 0_+}f(t)=f(0_+)=\lim_{s\rightarrow \infty}sF(s)\]

Note: 若 $F(s)$ 不是真分式，应化为真分式+多项式形式，$F(s)$ 是真分式.

9. 终值定理

若 $f(t)$ 及 $\dfrac{\mathrm{d}f(t)}{\mathrm{d}t}$ 可以进行拉氏变换，且 $f(t) \leftrightarrow F(s)$，则

\[f(\infty)=\lim_{t\rightarrow \infty}f(t)=\lim_{s\rightarrow 0}sF(s)\]

终值存在只有两种情况：

1. 极点都在 s 左半平面，终值为 0；
2. 单极点在 s=0，求终值相当于求部分分式展开式中 $\dfrac k s$ 项的系数 $k$.

10. s 域微分性质

若 $\mathscr{L}[f(t)]=F(s)$，则 $\mathscr{L}[tf(t)]=-\dfrac{\mathrm{d}F(s)}{\mathrm{d}s}$

推广：$\mathscr{L}[t^nf(t)]=(-1)^n\dfrac{\mathrm{d}^nF(s)}{ds^n}$

11. s 域积分性质*

若 $\mathscr{L}[f(t)]=F(s)$， 则 $\mathscr{L}[\dfrac{f(t)}{t}]=\int_s^\infty F(\lambda)\mathrm{d}\lambda$

要求 $\lim_{t \rightarrow 0} \dfrac 1 t f(t)$ 有界.

拉普拉斯逆变换

只介绍部分分式展开法：先展开成部分分式，再通过查典型信号拉氏变换表对应到原函数。

0. 预处理

能分离常数的，分离常数，例如 $F(s)=\dfrac{s}{s+2}=1-\dfrac 2{s+2}$

1. 单阶实极点

\[F(s)=\dfrac{A(s)}{(s-p_1)(s-p_2)\cdots(s-p_n)}=\dfrac{k_1}{s-p_1}+\dfrac{k_2}{s-p_2}+\cdots\dfrac{k_n}{s-p_n}\]

2. 多重极点

重根项的各阶分式都可能存在。

\[F(s)=\dfrac{A(s)}{(s-p_1)(s-p_2)^m}=\dfrac{k_1}{s-p_1}+\sum_{i=1}^m\dfrac{k_{2,i}}{(s-p_2)^i}\]

例：

\[F(s)=\dfrac{s^2}{(s+2)(s+1)^2}=\dfrac{k_1}{s+2}+\dfrac{k_2}{s+1}+\dfrac{k_3}{(s+1)^2}\]

$k_1, k_3$ 可以比较简单地4. 系数求解。

$k_2$ 需要做额外处理：等式两边同时乘 $(s+1)^2$。

\[\text{右边}=(s+1)^2\dfrac{k_1}{s+2}+k_2(s+1)+k_3\]

两边对 $s$ 求导

\[\text{右边}=\left[(s+1)^2\left(\dfrac{k_1}{s+2}\right)^\prime+2(s+1)\dfrac{k_1}{s+2}\right]+k_2\]

此时令 $s=-1, \text{右边}=k_2$

\[k_2=\text{左边}=\dfrac{\mathbf{d}}{\mathbf{ds}}\left[\dfrac{s^2}{s+2}\right]_{s=-1}=-3\]

3. 共轭复极点

若存在复极点，则必然以共轭对的形式出现，把共轭复极点写成指数加权的正弦项和余弦式变换式的组合。

\[F(s)=\dfrac{A(s)}{(s-p_1)[(s-\alpha)^2+\omega^2]}=\dfrac{k_1}{s-p_1}+\dfrac{k_2(s-\alpha)}{(s-\alpha)^2+\omega^2}+\dfrac{k_3\omega}{(s-\alpha)^2+\omega^2}\]

4. 系数求解

使用待定系数法和 Heaviside 掩盖法求解。

Heaviside掩盖法

\[k_i=F(s)(s-p_i) \vert _{s=p_i}\]

注意，其中 $s-p_i$ 是通常情况下，这里实际上指的是 $k_i$ 那一项的分母，同时还要注意分子不只有 $k_i$ 的情况需要特殊处理。

5. 包含冲激项（假分式）的

先把假分式展开为正幂函数多项式和真分式相加的形式，再进行运算。

例如 $F(s)=\dfrac{s^3+5s^2+9s+7}{s^2+3s+2}=s+2+\dfrac{s+3}{s^2+3s+2}$

6. 包含时移项的

时移项 $e^{-\alpha s}$ 要最后处理，对整个函数（包括 $u(t)$）进行时移。

例如 $F(s)=\dfrac{e^{-2s}}{s^2+3s+2}=\dfrac 1{s+1}-\dfrac 1{s+2}$ ， $f(t)=\left[e^{-(t-2)}-e^{-2(t-2)}\right]u(t-2)$

拉普拉斯变换求解微分方程

方程两边做拉氏变换。注意：

\[\mathscr{L}\left[\dfrac{\mathbf{d}f(t)}{\mathbf{d}t}\right]=sF(s)-f(0_-)\] \[\mathscr{L}\left[\dfrac{\mathbf{d}^2f(t)}{\mathbf{d}t^2}\right]=s[sF(s)-f(0_-)]-f^\prime(0_-)\]

然后计算出全响应 $R(s)=A(S)E(S)+C_1(s)r(0-)+C_2(s)r^\prime(0-)+\cdots$

其中零状态响应

\[R{zs}(s)=A(S)E(S)\]

零输入响应 \(R_{zi}(s)=C_1(s)r(0_-)+C_2(s)r^\prime(0_-)+\cdots\)

拉普拉斯变换分析电路

电路的 $s$ 域模型

电阻

阻抗：$R$

$V_R(s)=RI_R(s)$

模型和时域相同。

电感

\[e_L(t)=L\dfrac{\mathbf{d}i_L(t)}{\mathbf{d}t}\]

感抗：$Ls$

\[V_L(s)=sLI_L(s)-Li_L(0_-)=Ls(I_L(s)-\dfrac{i_L(0_-)}{s})\]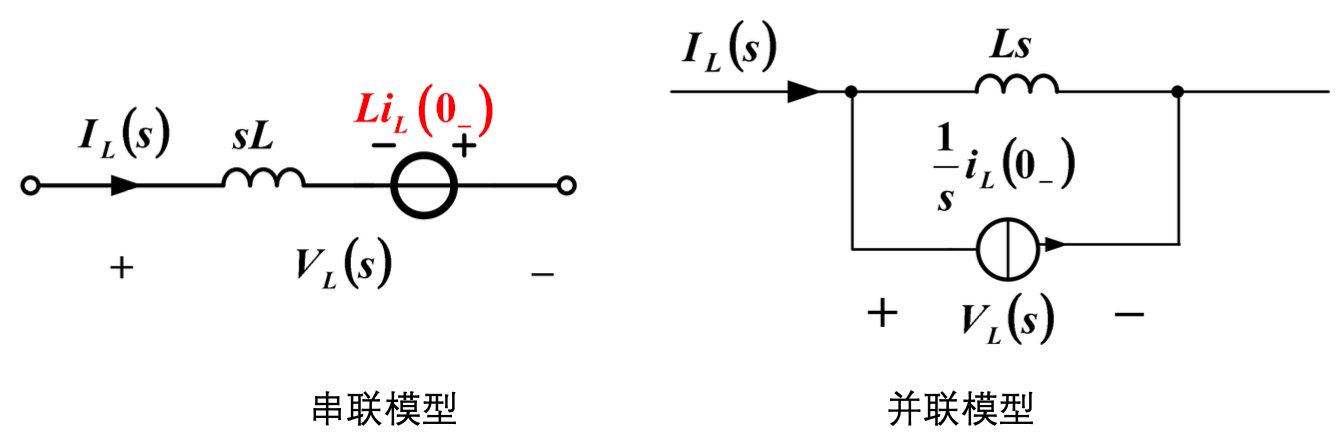

电容

\[i_C(t)=C\dfrac{\mathbf{d}v_C(t)}{\mathbf{d}t}\]

容抗： $\dfrac 1 {sC}$

\[V_C(s)=\dfrac 1{sC}I_C(s)+\dfrac{v_C(0_-)}{s}=\dfrac 1 {sC}\left[I_C(s)+Cv_c(0_-)\right]\]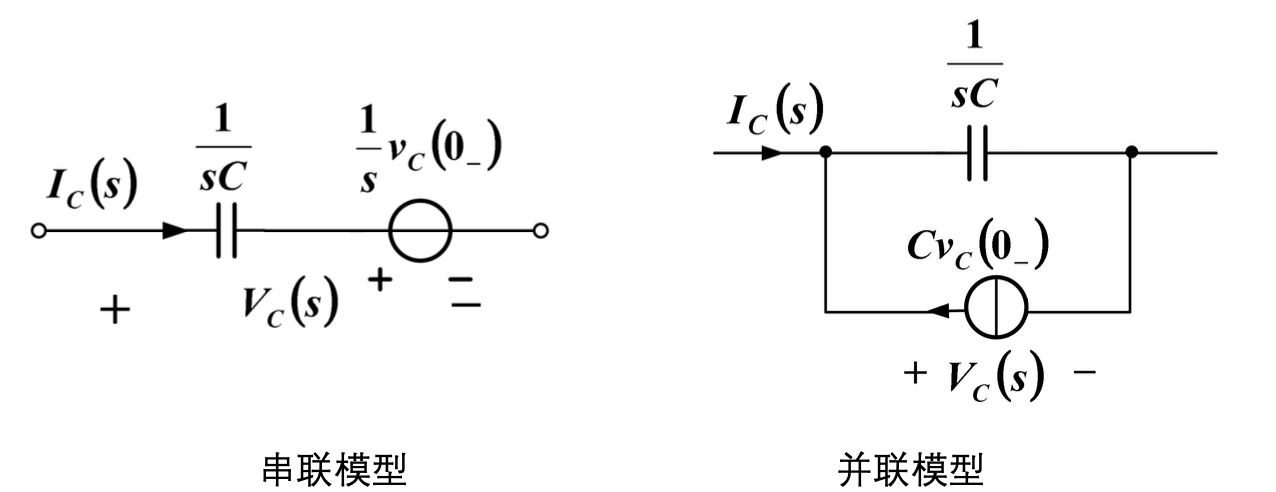

连续系统的稳定性

时域判定方法：系统的单位冲激响应绝对可积 $\int_{-\infty}^{\infty}\vert h(t) \vert \mathbf{d} t \le M$ s 域判定方法：$H(s)$ 的收敛域包含虚轴。

因果系统稳定性判定方法

1. 稳定系统：全部极点位于 s 平面的左半平面（不包含虚轴）
2. 不稳定系统：有极点位于右半平面，或在虚轴上有二阶及以上极点
3. 临界稳定（不稳定系统）：极点在虚轴上且只有一阶

拉普拉斯变换和傅氏变换的关系

收敛域为 $\sigma > \sigma_0$

1. $\sigma_0 > 0$，收敛轴位于 $s$ 平面的右半平面，则 $F(j\omega)$ 不存在
2. $\sigma_0 < 0$，收敛轴位于 $s$ 平面的左半平面，则 \(F(j\omega=F(s)|_{s=j\omega}\)
3. $\sigma_0=0$，收敛轴位于虚轴，则 \(F(j\omega=F(s)|_{s=j\omega}+\pi\sum_{n}k_n\delta(\omega-\omega_n)\)

时域信号	拉普拉斯变换	傅里叶变换
$u(t)$	$\dfrac 1 s$	$\dfrac 1 {j\omega}+\pi\delta(\omega)$
$\sin(\omega_0t)u(t)$	$\dfrac{\omega_0}{s^2+\omega_0^2}$	$\dfrac{\omega_0}{(jw)^2+\omega_0^2}+\dfrac{j\pi}2\left[\delta(\omega+\omega_0)-\delta(\omega-\omega_0)\right]$
$tu(t)$	$\dfrac 1{s^2}$	$\dfrac{1}{(j\omega)^2}+j\pi\delta^\prime(\omega)$